Introduction
The Wordle Craze has inspired many spinoff -le games.
One of the Wordle spinoffs me and my friends have recently gotten into is Nerdle. It’s very similar to Wordle except you attempt to guess an equation which consists of \(\{ 0-9, +, \times, /, -, = \}\).
Let’s try to write an algorithm for solving this game!
First attempt
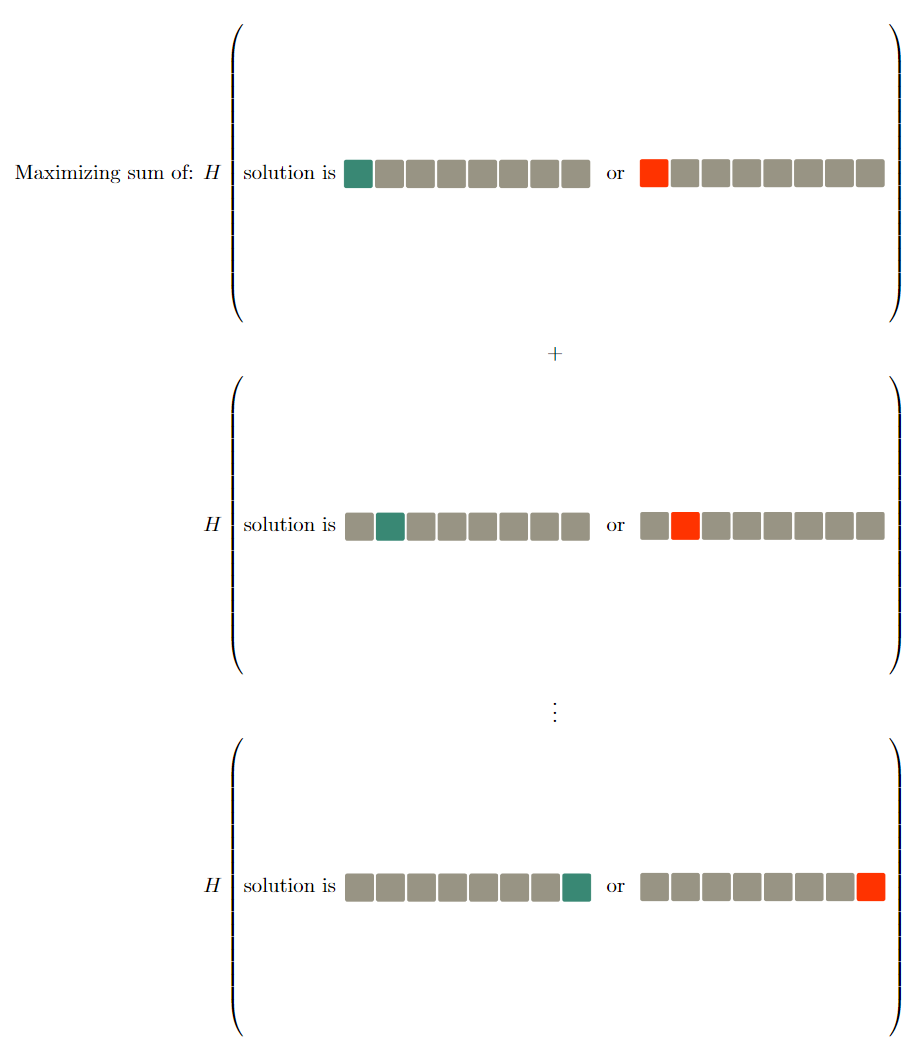
For the first attempt I wrote an algorithm which assumes the optimal guess is the one which maximizes the following equation:
Where a green tile indicates that the guess is correct (i.e. the solution also has that character for the selected tile), a red tile indicates that the guess is wrong (but that character may or may not be somewhere else) and grey means the character was ignored for that calculation.
We can express this algorithm in more technical terms:
\[H(x) = \sum_{i=0}^7{( -log_2{(\frac{|E_i(x_i)|}{n})} * \frac{|E_i(x_i)|}{n} + -log_2{(\frac{|{NE}_i(x_i)|}{n})} * \frac{|{NE}_i(x_i)|}{n} )}\]Where:
\[\begin{align} N &= \text{Our possible solution set} \\ x &\in N \\ n &= |N| \\ E_x(c) &= \{s \in N | s_x = c_x \} \\ NE_x(c) &= \{s \in N | s_x \neq c_x \} \\ H(x) &= \text{entropy or information of x} \ \end{align}\]According to this algorithm, the optimal first guess would have been \(30-11=19\) which anyone familiar with Wordle can tell is a bad guess due to the fact that \(1\) is used multiple times.
So, what’s going on? Well, the above algorithm is really just trying to maximize the information obtained by knowing if a character is in a specific spot or not. This is essentially the same as picking a guess which contains the most common character per column.
We can verify this by plotting the most popular characters for each possible solution. This code provides us the following distribution:
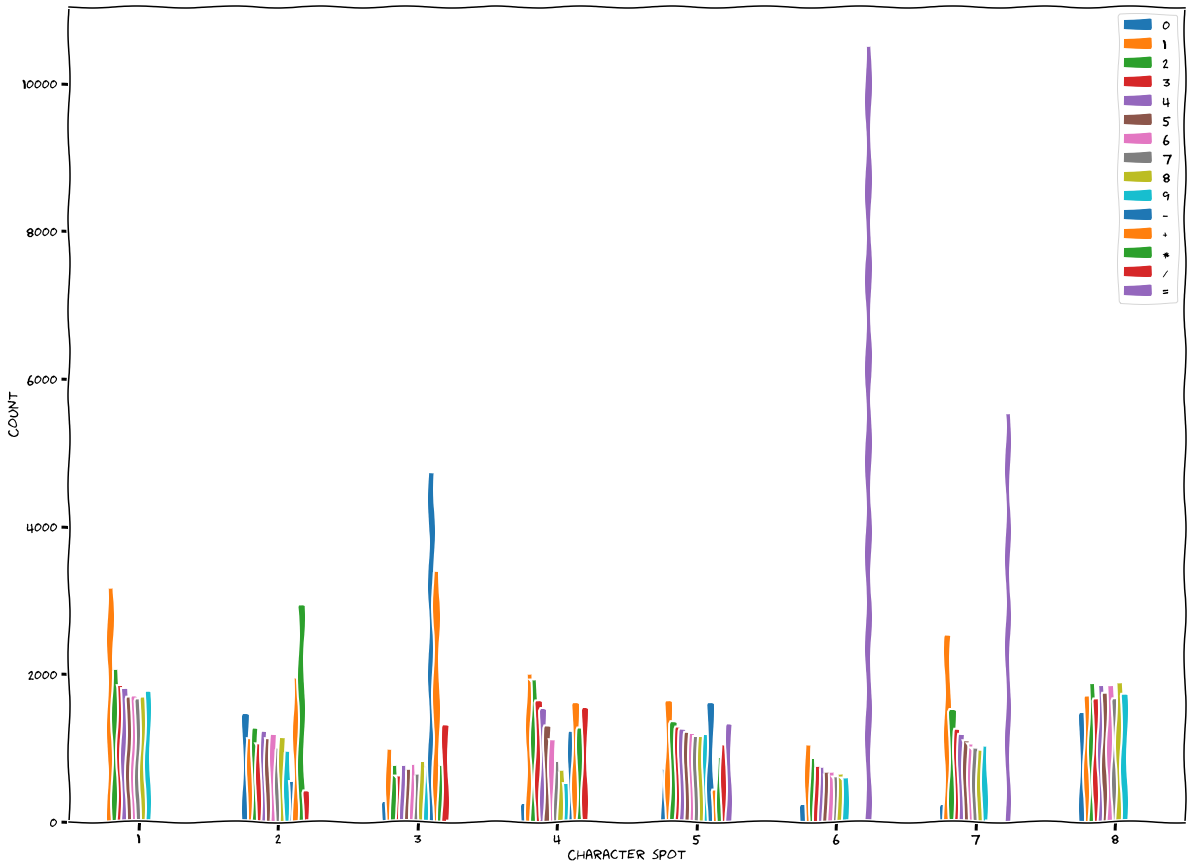
We can see quite clearly that each of the “optimal” guess’s slots are filled with one of the top three characters.
While this algorithm does usually succeed in solving a Nerdle, it tends to take upwards of 4 or 5 guesses, which seems quite excessive. Let’s see if we can do better.
Second attempt
While showing my first attempt at solving Nerdle to a friend, he mentioned that 3Blue1Brown had made a video describing the optimal strategy for Wordle. 3B1B was also using entropy and information theory; the key difference was what he was calculating the entropy of.
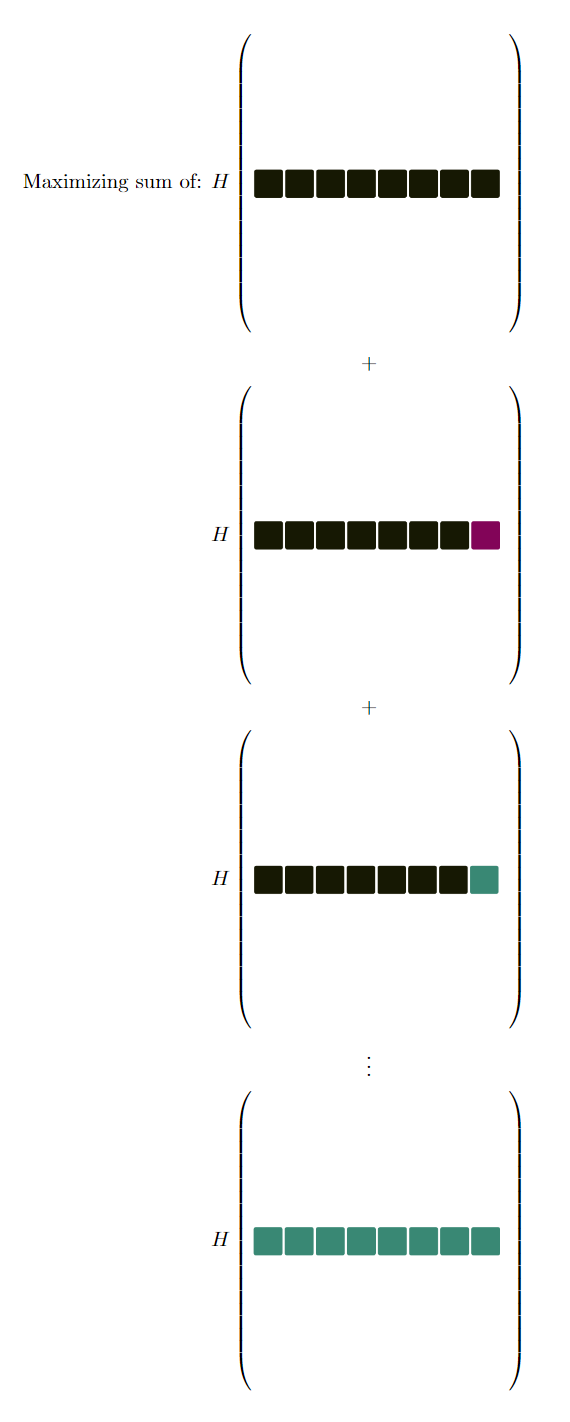
After you provide the game an answer the game automatically marks which characters are in the right place. In the case of Nerdle, it uses Green (indicating the character was correct), Purple (indicating the solution has that character, but not in that spot) and Black (indicating that character is not used within the solution).
Since the answer consists of 8 characters, there are \(3^8\) possible patterns that the computer can mark. Instead of calculating the entropy around whether a solution has a specific character in a specific spot, we’ll calculate the entropy over the distribution of solutions within these possible patterns.
This approach will favor a guess which has a flat distribution for the \(3^8\) possible patterns. Why is this optimal? Imagine two different cases
- guess \(A\) highly favors \(2\) of the possible distributions,
- guess \(B\) which equally favors all \(3^8\) distributions.
While guess \(A\) does seem decent (after all, both distributions indicate we are halfway there) since we are only splitting the solution set in half it’s actually quite ineffective. Imagine the solution set started with \(1,000,000\) possible solutions. Guess \(A\) would leave us with \(1,000,000 * \frac{1}{2} = 500,000\) solutions. Not the greatest reduction.
Guess \(B\) will cut the possible solution set by a factor of \(\frac{1}{3^8} \approxeq 0.000152415790276\). Meaning the initial solution set will be cut down to \(1,000,000 * \frac{1}{3^8} \approxeq 153\) possible solutions. A huge reduction in comparison to guess \(A\).
Since guess \(B\) has equal splits across all possible patterns then regardless of which pattern ends up being revealed by the game we know that we’ve maximized the number of solutions we can discard and are no longer prevalent.
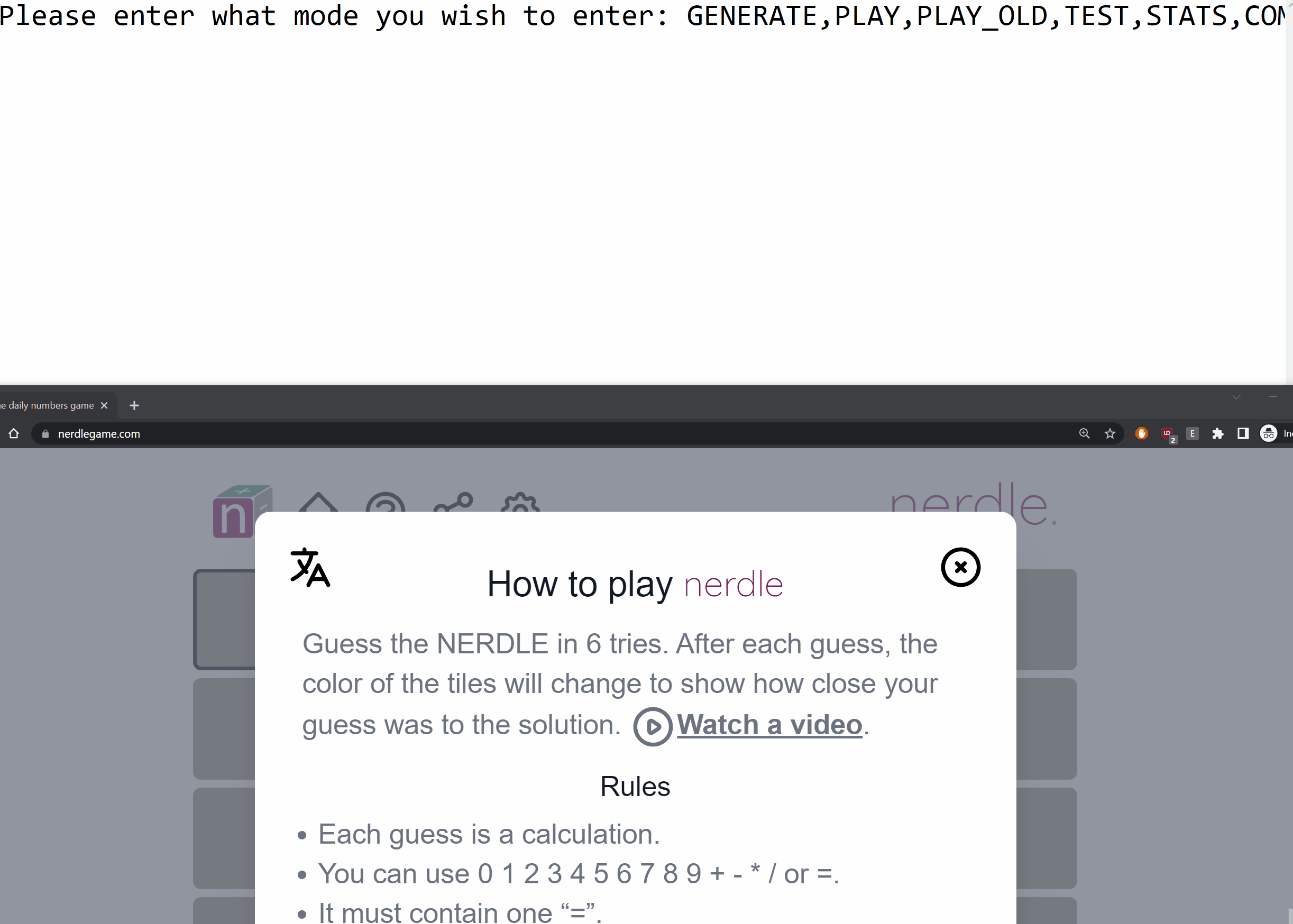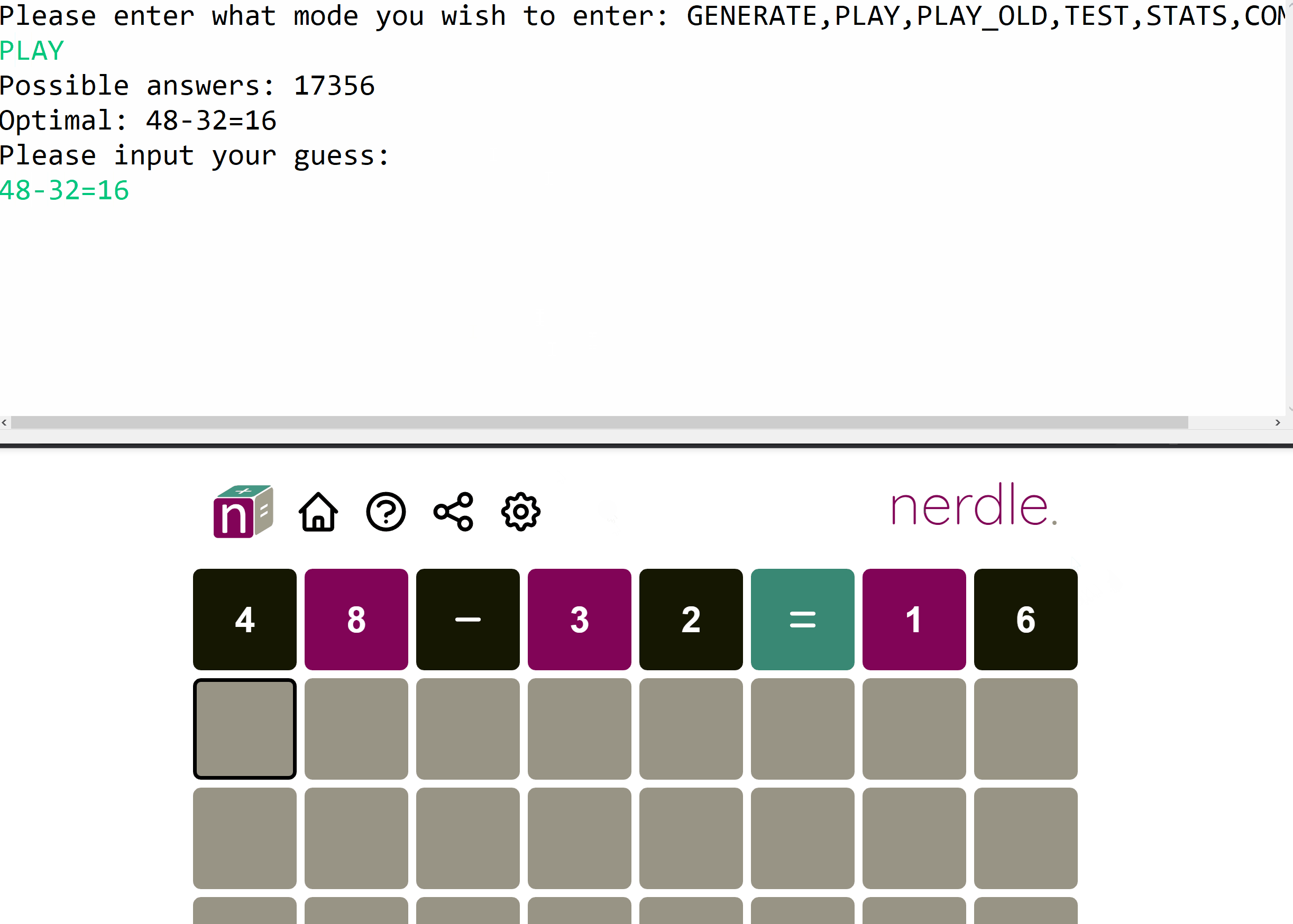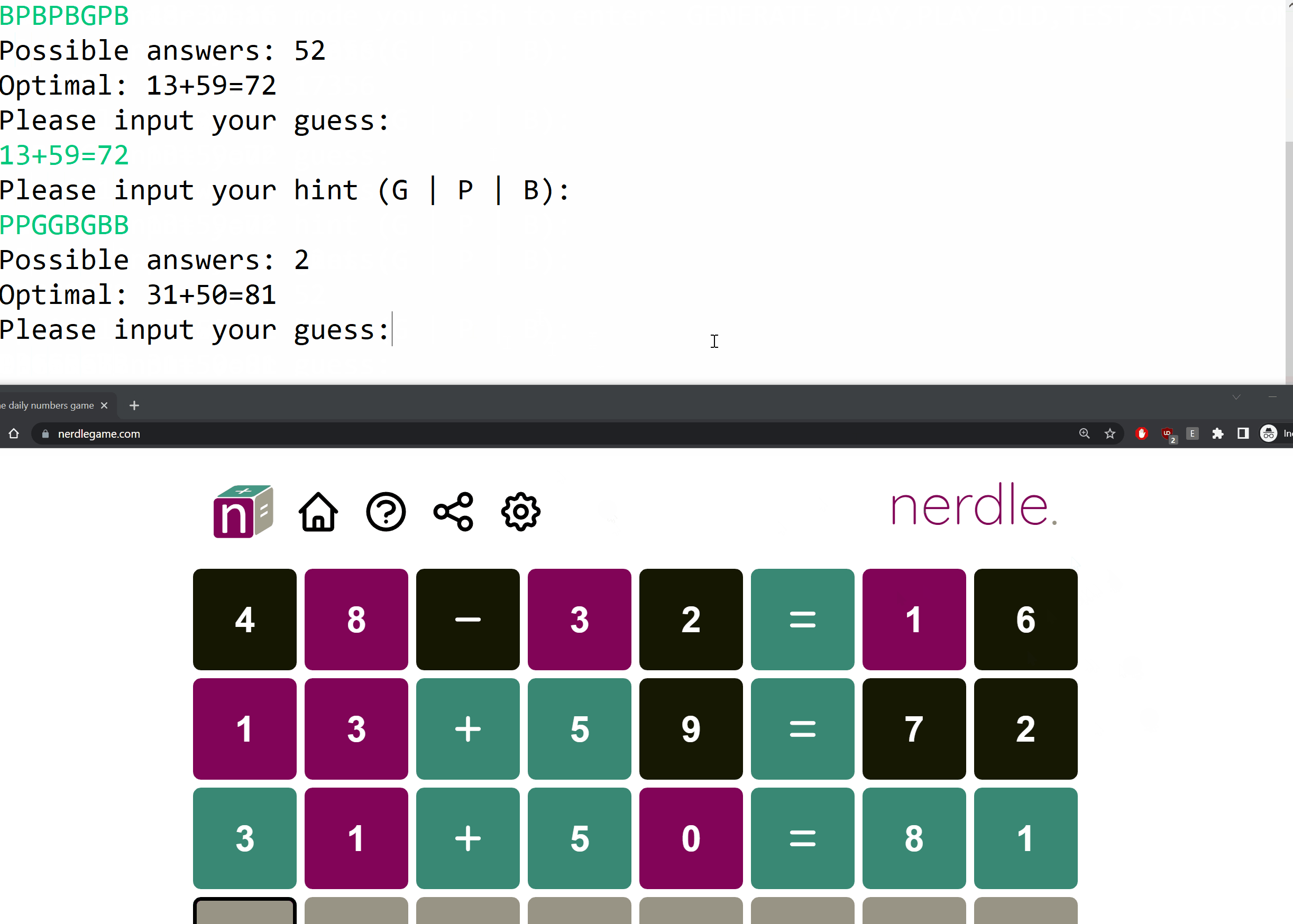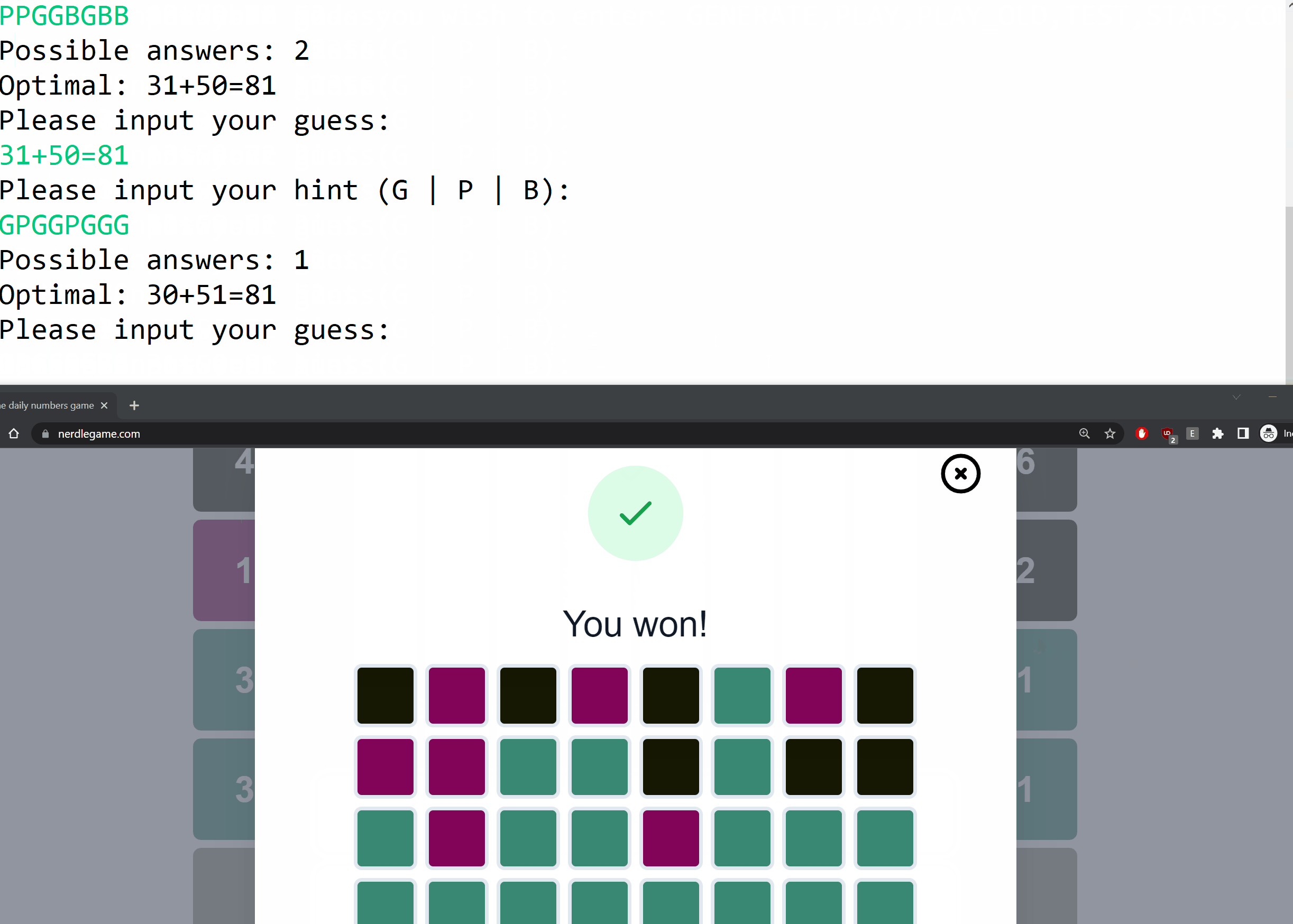
This algorithm computed that \(48-32=16\) was the optimal guess. Which seems quite reasonable as there is no reuse of characters.
Pitting this algorithm against Nerdle typically yields a solution within \(2-3\) guesses which I think is quite good. In the 3B1B video, there are discussions on how to further improve the algorithm (calculating the entropy on the next guess) which could be interesting to implement and see how that modifies the optimal guess.
Code
The code is available here and here’s a sample run of the program.