Introduction
In Jane Street’s latest puzzle, Beside the Point, we’re given the following prompt
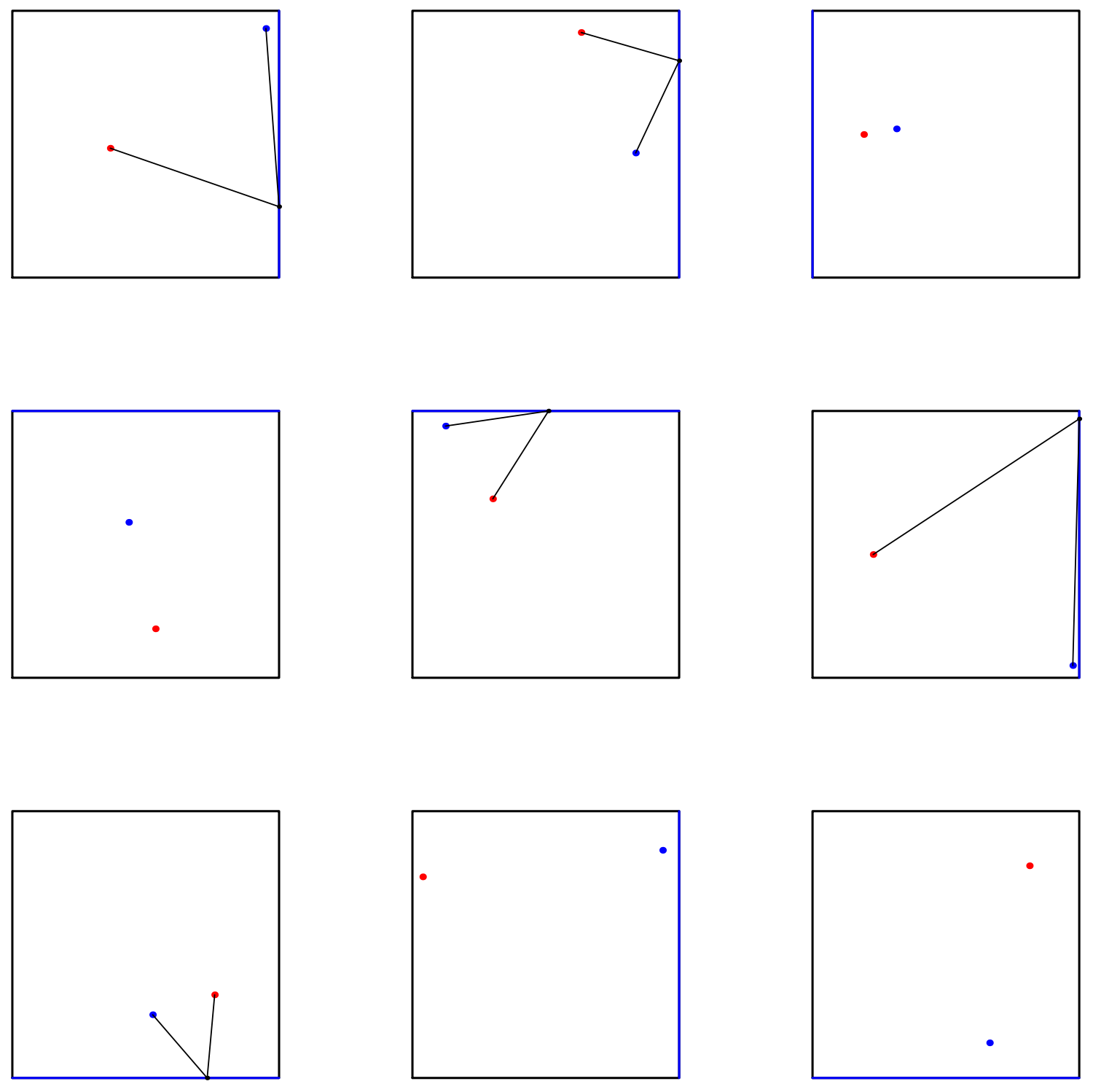
Two random points, one red and one blue, are chosen uniformly and independently from the interior of a square. To ten decimal places, what is the probability that there exists a point on the side of the square closest to the blue point that is equidistant to both the blue point and the red point?
As well as a visual depiction
Solution
point on the side of the square closest to the blue point that is equidistant to both the blue point and the red point
Without loss of generality let’s assume the blue point is within the triangle defined by \((0,0), (0.5,0.5) \textrm{ and } (1,0)\). To find an equidistant point we can envision a circle with a centroid at \((a, 0)\) (i.e. on the x-axis) and the red and blue points lying on the circle’s border.
If we are given two points we can determine \(a\) via the following equation:
\[\begin{aligned} P_{blue} = P_b &= (x_1, y_1) \\ P_{red} = P_r &= (x_2, y_2) \\ \textrm{Circle Centroid} &= (a, 0) \textrm{ s.t. } 0 \leq a \leq 1 \\ (x_1 - a)^2 + (y_1 - 0)^2 &= r^2 \\ (x_2 - a)^2 + (y_2 - 0)^2 &= r^2 \\ \end{aligned}\] \[\begin{aligned} (x_1 - a)^2 + (y_1 - 0)^2 &= (x_2 - a)^2 + (y_2 - 0)^2 \\ (x_1 - a)^2 + y_1^2 &= (x_2 - a)^2 + y_2^2 \\ (x_1 - a)^2 - (x_2 - a)^2 &= y_2^2 - y_1^2 \\ x_1^2 - 2x_1a - a^2 - x_2^2 + 2x_2a + a^2 &= y_2^2 - y_1^2 \\ x_1^2 - x_2^2 - 2x_1a + 2x_2a &= y_2^2 - y_1^2 \\ -2x_1a + 2x_2a &= y_2^2 - y_1^2 - x_1^2 + x_2^2 \\ 2a(x_2 - x_1) &= y_2^2 - y_1^2 - x_1^2 + x_2^2 \\ a &= \frac{(y_2^2 - y_1^2 - x_1^2 + x_2^2)}{2(x_2 - x_1)} \\ \end{aligned}\]Which gives us the equation for the circle, with \((a,0)\) as it’s centroid and the blue/red point lying on the border, as
\[(x - a)^2 + y^2 = (a - x_1)^2 + (0-y)^2\]We can represent the area for which \(a\) is defined (when give the blue point) as the area of the following circles:
\[x ^ 2 + y^2 = x_1^2 + y^2 \\ x^2 + y^2 -2x = x_1^2 +y_1^2 - 2x_1\]
The above clip visually shows how the two circles defined above encompass the entire valid area for the red point. You can play with the demo yourself here.
The intersection of these two circles needs to be removed (formulas taken from here)
\[r_1 = \sqrt{(x_1^2 + y_1^2)} \\ r_2 = \sqrt{((x_1-1)^2 + y_1^2)} \\ c_{bd} = 2 * \arccos{\frac{r_2^2 + 1 - r_1^2}{2r_2}} \\ c_{ad} = 2 * \arccos{\frac{r_1^2 + 1 - r_2^2}{2r_0}} \\ \textrm{intersection area} = \frac{1}{2}r_2^2(c_{bd} - \sin(c_{bd})) + \frac{1}{2}r_1^2(c_{ad} - \sin(c_{ad}))\]Therefore given a blue point the probability that there exists a point on the side of the square that is equidistant to both the blue point and the red point is:
\[P = \textrm{Area of the circle defined by a = 0} + \textrm{Area of the circle defined by a = 1} - \textrm{intersection area} \\ = \frac{pi * r_1^2}{4} + \frac{pi * r_2^2}{4} - \textrm{intersection area}\]To find the general probability (i.e. given any blue point) we can do a double integration
\[8 * \int_0^{0.5}{\int_0^{x} \frac{\pi r_1^2}{4} + \frac{\pi r_2^2}{4} - \textrm{intersection area } dy dx}\]Which we can use scipy to integrate:
from scipy import integrate
import numpy as np
f_r1 = lambda x,y: np.sqrt(x * x + y * y)
f_r2 = lambda x,y: np.sqrt((x-1.0) * (x-1.0) + y * y)
f_cbd = lambda r0, r1: 2 * np.arccos( (r1 * r1 + 1 - r0 * r0) / (2 * r1 ))
f_cad = lambda r0, r1: 2 * np.arccos( (r0 * r0 + 1 - r1 * r1) / (2 * r0 ))
f_intersection = lambda r0, r1, cbd, cad: (1/2) * cbd * r1 * r1 - 1/2 * r1 * r1 * np.sin(cbd) \
+ (1/2) * cad * r0 * r0 - (1/2) * r0 * r0 * np.sin(cad)
f_area = lambda y,x: (np.pi * f_r1(x,y) * f_r1(x,y) / 4.0) + \
(np.pi * f_r2(x,y) * f_r2(x,y) / 4.0) - \
f_intersection(
f_r1(x,y),
f_r2(x,y),
f_cbd(f_r1(x,y), f_r2(x,y)),
f_cad(f_r1(x,y), f_r2(x,y))
)
res = integrate.dblquad(f_area, 0, 0.5, 0, lambda x: x)
print(res[0] * 8, res[1])
# 0.49140757883830793 2.485643838466147e-15
Providing a final answer of 0.4914075788
Brute force
We can double check this by performing trillions of trial runs:
- Generate a random point within the triangle defined as \(ABC\)
- Generate a random independent point in the unit square
- Calculate \(a\) as shown above
- If \(a\) is between 0 and 1 (inclusive on both ends) increment the success counter
- Increment the trial counter
- Print (success / trial)
public static void bruteMiniForce() {
int counter = 0;
BigDecimal trials = BigDecimal.ZERO;
BigDecimal success = BigDecimal.ZERO;
double x1 = 0, y1 = 0, x2 = 0, y2 = 0;
double r1 = 0, r2 = 0;
Random r = new Random();
while(true) {
r1 = r.nextDouble();
r2 = r.nextDouble();
x2 = r.nextDouble();
y2 = r.nextDouble();
if(r1 == 0 || r2 == 0 || x2 == 0 || y2 == 0) continue;
// https://stackoverflow.com/questions/19654251/random-point-inside-triangle-inside-java
// x = (1 - Math.sqrt(r1)) * 0 + (Math.sqrt(r1) * (1 - r2)) * 0.5 + (Math.sqrt(r1) * r2) * 1;
x1 = (Math.sqrt(r1) * (1 - r2)) * 0.5 + (Math.sqrt(r1) * r2) * 1;
// y = (1 - Math.sqrt(r1)) * 0 + (Math.sqrt(r1) * (1 - r2)) * 0.5 + (Math.sqrt(r1) * r2) * 0;
y1 = (Math.sqrt(r1) * (1 - r2)) * 0.5;
double centroid = (x2 * x2 - x1 * x1 + y2 * y2 - y1 * y1) / (2 * (x2 - x1));
if(centroid >= 0 && centroid <= 1) success = success.add(BigDecimal.ONE);
trials = trials.add(BigDecimal.ONE);
counter++;
if(counter == 1_000_000_000) {
counter = 0;
System.out.println(trials + " " + (success.divide(trials, MathContext.DECIMAL64).doubleValue()));
}
}
}
Which after 195_000_000_000 trials provides a probability of 0.4914080657435897. Only differing from the correct answer at the 6th decimal digit.