Introduction
In Jane Street’s latest puzzle, Hall of Mirrors 3, we’re given the following prompt
The perimeter of a 10-by-10 square field is surrounded by lasers pointing into the field. (Each laser begins half a unit from the edge of the field, as indicated by the •’s.)
Some of the lasers have numbers beside them. Place diagonal mirrors in some of the cells so that the product of the segment lengths of a laser’s path matches the clue numbers. (For instance, the segments for the “75” path in the example puzzle have lengths 5, 3, 5.) Mirrors may not be placed in orthogonally adjacent cells.
Once finished, determine the missing clue numbers for the perimeter, and calculate the sum of these clues for each side of the square. The answer to this puzzle is the product of these four sums.
As well as a visual depiction
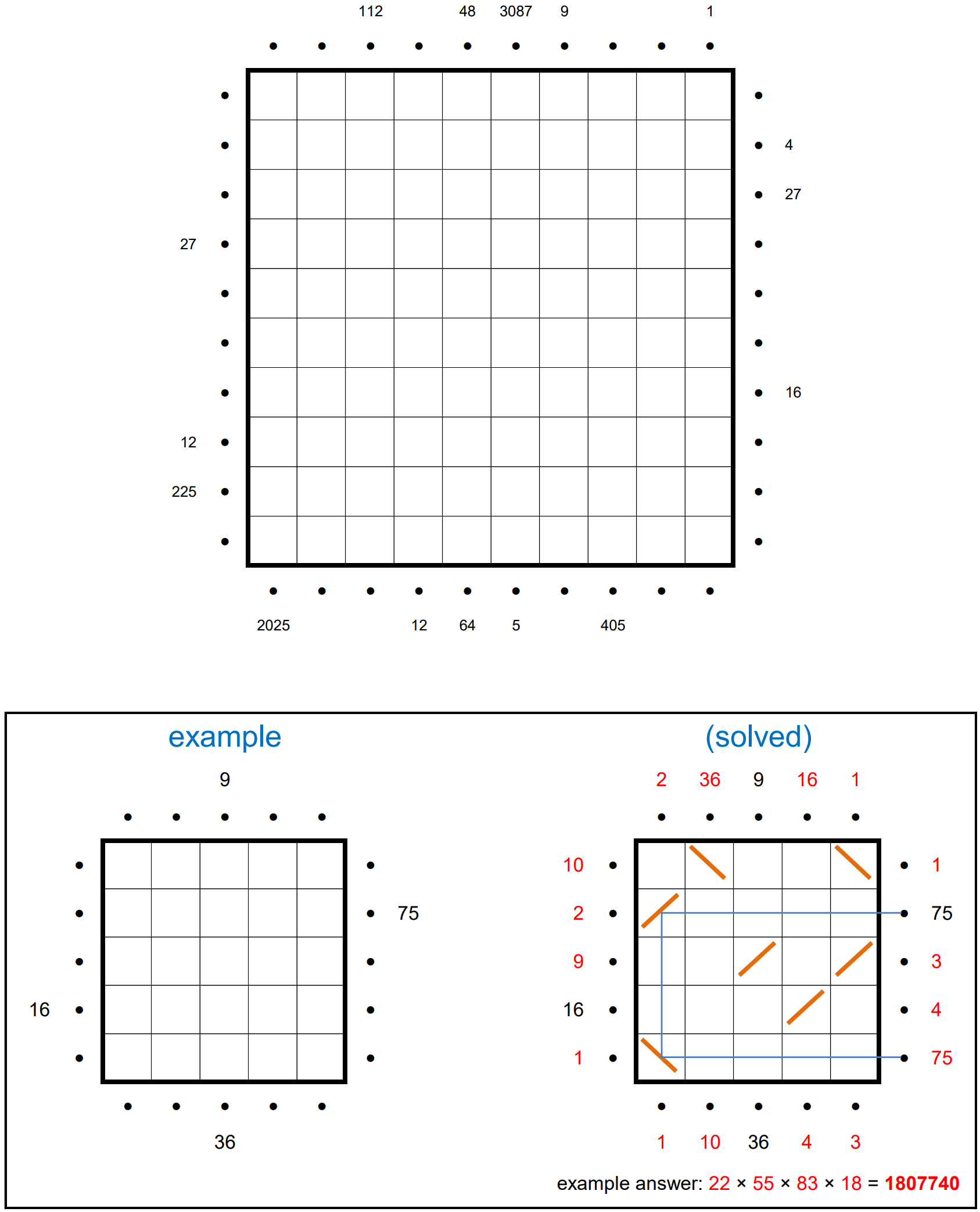
Solution
A brute force (backtracking) solution works sufficiently well with the size of the search space. For each given starting point we construct a series of gates that meet the clue numbers, the traversed squares are kept track of and new gates are only placed on untraversed squares.
package janestreet;
import java.util.Arrays;
import java.util.stream.LongStream;
public class hall_of_mirrors_3 {
// 0 - blank
// 1 - \
// 2 - /
static int[][] exampleBoard = new int[][] {
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
{ 0, 0, 0, 0, 0 },
};
static int[][] realBoard = new int[][] {
{0, 0, 0, 0, 0, 0, 0, 0, 0, 1},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
};
// startRow, startColumn, expectedValue, directionRow, directionCol
static int[][] exampleStartingPoints = new int[][] {
{ 0, 2, 9, 1, 0 },
{ 1, 4, 75, 0, -1 },
{ 3, 0, 16, 0, 1 },
{ 4, 2, 36, -1, 0}
};
static int[][] realStartingPoints = new int[][] {
{ 0, 2, 112, 1, 0 },
{ 0, 4, 48, 1, 0 },
{ 0, 5, 3087, 1, 0 },
{ 0, 6, 9, 1, 0 },
{ 0, 9, 1, 1, 0 },
{ 3, 0, 27, 0, 1 },
{ 7, 0, 12, 0, 1 },
{ 8, 0, 225, 0, 1 },
{ 1, 9, 4, 0, -1 },
{ 2, 9, 27, 0, -1 },
{ 6, 9, 16, 0, -1 },
{ 9, 0, 2025, -1, 0 },
{ 9, 3, 12, -1, 0 },
{ 9, 4, 64, -1, 0 },
{ 9, 5, 5, -1, 0 },
{ 9, 7, 405, -1, 0 },
};
static int[][] board = realBoard;
static int[][] startingPoints = realStartingPoints;
// static int[][] board = exampleBoard;
// static int[][] startingPoints = exampleStartingPoints;
static boolean[][] traversed = new boolean[board.length][board.length];
public static void main(String[] args) {
solve(0, startingPoints[0][0], startingPoints[0][1], startingPoints[0][2],
startingPoints[0][3], startingPoints[0][4], 1, 1);
}
public static void solve(
int index,
int r,
int c,
int expectedValue,
int dirR,
int dirC,
int curr,
int total) {
if(r < 0 || c < 0 || r >= board.length || c >= board.length) {
if(expectedValue == total * curr) {
// possible solution
if(index + 1 == startingPoints.length) {
printSolution();
} else {
solve(index + 1, startingPoints[index + 1][0],
startingPoints[index + 1][1], startingPoints[index + 1][2],
startingPoints[index + 1][3], startingPoints[index + 1][4], 1, 1);
}
}
return;
}
if(total * curr > expectedValue) return;
if(board[r][c] != 0) {
// gate already down we have to follow it
if(board[r][c] == 1) {
solve(index, r + dirC, c + dirR, expectedValue, dirC, dirR, 1, total * curr);
} else if(board[r][c] == 2) {
solve(index, r - dirC, c - dirR, expectedValue, -dirC, -dirR, 1, total * curr);
}
} else {
// leave empty, continue in the same direction
boolean pastTraversed = traversed[r][c];
traversed[r][c] = true;
solve(index, r + dirR, c + dirC, expectedValue, dirR, dirC, curr + 1, total);
// validate placing this gate doesn't break previous patterns
if(!pastTraversed && noOrthoganelGates(r, c)) {
// place 1 gate
board[r][c] = 1;
solve(index, r + dirC, c + dirR, expectedValue, dirC, dirR, 1, total * curr);
// place 2 gate
board[r][c] = 2;
solve(index, r - dirC, c - dirR, expectedValue, -dirC, -dirR, 1, total * curr);
board[r][c] = 0;
}
traversed[r][c] = pastTraversed;
}
}
public static boolean noOrthoganelGates(int r, int c) {
boolean left = r - 1 > 0 ? board[r - 1][c] != 0 : false;
boolean right = r + 1 < board.length ? board[r + 1][c] != 0 : false;
boolean up = c - 1 > 0 ? board[r][c - 1] != 0 : false;
boolean down = c + 1 < board.length ? board[r][c + 1] != 0 : false;
return !left && !right && !up && !down;
}
public static void printSolution() {
System.out.println("Found a solution");
for(int[] i: board) System.out.println(Arrays.toString(i));
long[] top = LongStream.range(0, board.length)
.filter(i -> Arrays.stream(startingPoints).noneMatch(p -> p[0] == 0 && p[1] == i
&& p[3] == 1 && p[4] == 0))
.map(i -> traverse(0, (int)i, 1, 0, 1L, 1L)).toArray();
long[] bottom = LongStream.range(0, board.length)
.filter(i -> Arrays.stream(startingPoints).noneMatch(p -> p[0] == board.length - 1 && p[1] == i
&& p[3] == -1 && p[4] == 0))
.map(i -> traverse(board.length - 1, (int)i, -1, 0, 1L, 1L)).toArray();
long[] left = LongStream.range(0, board.length)
.filter(i -> Arrays.stream(startingPoints).noneMatch(p -> p[0] == i && p[1] == 0
&& p[3] == 0 && p[4] == 1))
.map(i -> traverse((int)i, 0, 0, 1, 1L, 1L)).toArray();
long[] right = LongStream.range(0, board.length)
.filter(i -> Arrays.stream(startingPoints).noneMatch(p -> p[0] == i && p[1] == board.length - 1
&& p[3] == 0 && p[4] == -1))
.map(i -> traverse((int)i, board.length - 1, 0, -1, 1L, 1L)).toArray();
System.out.println(Arrays.toString(top));
System.out.println(Arrays.toString(bottom));
System.out.println(Arrays.toString(left));
System.out.println(Arrays.toString(right));
System.out.println("Final answer: " + Arrays.stream(top).sum() *
Arrays.stream(bottom).sum() *
Arrays.stream(left).sum() *
Arrays.stream(right).sum());
}
public static long traverse(int r, int c, int dirR, int dirC, long curr, long total) {
if(r < 0 || c < 0 || r >= board.length || c >= board.length) {
return curr * total;
}
// follow gate
if(board[r][c] != 0) {
if(board[r][c] == 1) {
return traverse(r + dirC, c + dirR, dirC, dirR, 1, total * curr);
} else if(board[r][c] == 2) {
return traverse(r - dirC, c - dirR, -dirC, -dirR, 1, total * curr);
}
}
return traverse(r + dirR, c + dirC, dirR, dirC, curr + 1, total);
}
}